Câu đố tìm đường cho cô gái làm khó người giải

Câu đố như sau:

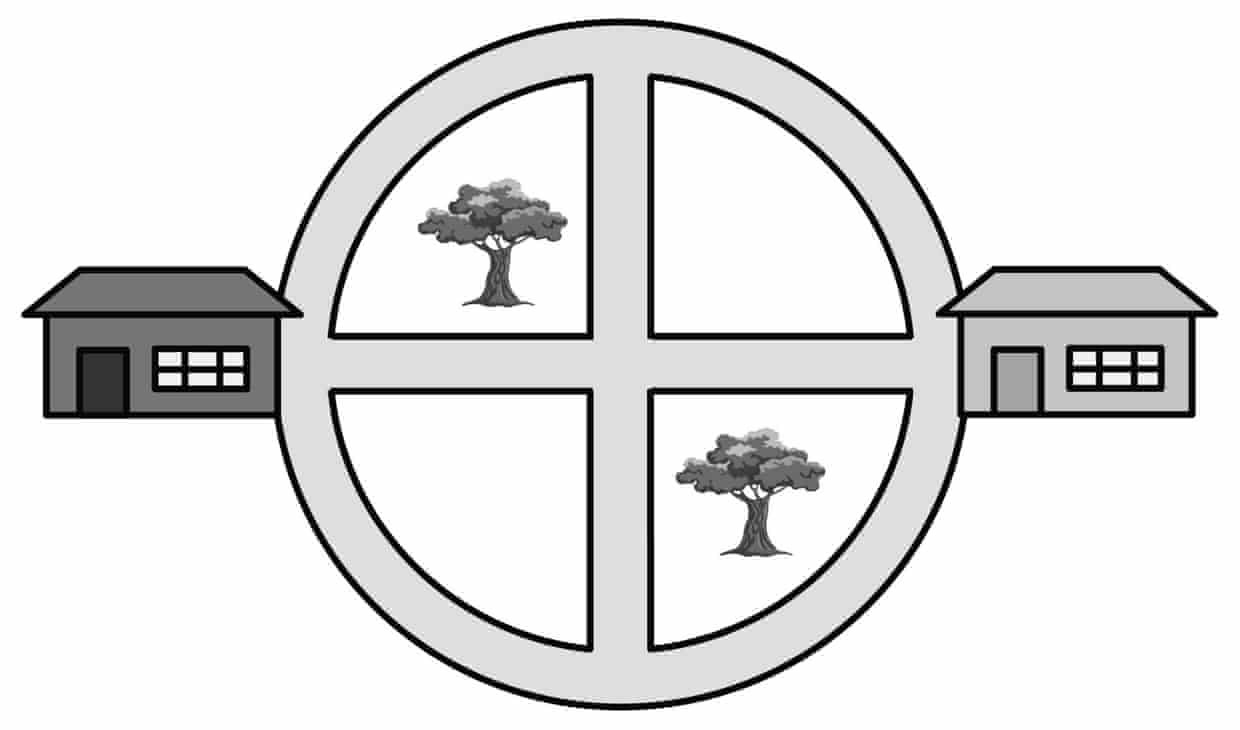Mỗi buổi chiều, Jogger Jane chạy từ nhà (bên trái) đến trường (bên phải).

Bốn con đường thẳng dài 1 km, 4 cung đường cong dài 1,5 km/cung. Mỗi lần chạy, Jane luôn chạy hơn 3 km và trong một buổi chạy, cô ấy không bao giờ đi trên một con đường hai lần.

Ngoài ra, cô cũng không cần chạy hết tất cả con đường trong một lần. Cô có thể đi ngang qua nhà mình và kết thúc buổi chạy tại trường.

Theo bạn, với các yêu cầu trên, Jogger Jane có thể chọn bao nhiêu tuyến đường khác nhau? Đương nhiên, như đã nói từ đầu, cô ấy có trên 10 cách chạy.

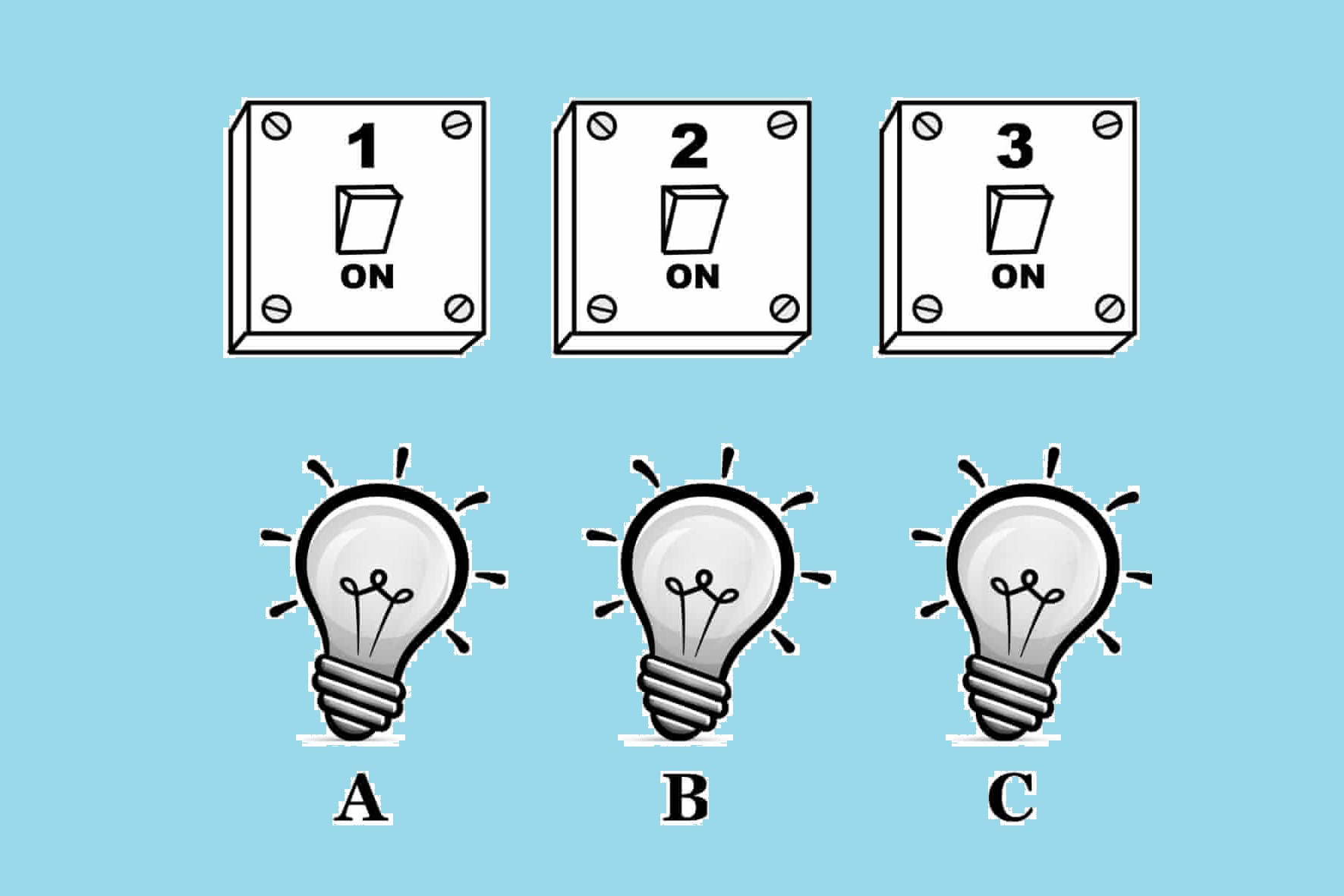
Trước đó, ngày 2/1, Tri thức - Znews giới thiệu câu đố bạn có đủ thông minh để gia nhập Mensa về xác định công tắc - bóng đèn. Đáp án như sau:

Ba nhận định gồm:

1. Công tắc 1 điều khiển bóng đèn B.

2. Công tắc 2 điều khiển bóng đèn A hoặc C.

3. Công tắc 3 điều khiến bóng đèn A hoặc B.

Theo đề bài, chỉ một nhận định đúng. Dùng phương pháp loại trừ, ta xác định được câu thứ 3 đúng.

Cụ thể, nếu câu đầu tiên đúng, hai câu còn lại phải sai. Tuy nhiên, nếu đúng là công tắc 1 điều khiển bóng đèn B, công tắc 2 chắc chắn phải kết nối với bóng đèn A hoặc C. Tức câu 2 cũng đúng. Điều này trái với đề bài (chỉ 1 trong 3 câu đúng).

Nếu câu 2 đúng, công tác 2 điều khiển A hoặc C. Hai câu còn lại phải sai tức công tác 1 điều khiển bóng đèn A hoặc C, công tắc 3 điều khiển bóng đèn C. Điều này đồng nghĩa không có công tắc nào nối với bóng đèn B - trái với yêu cầu đề bài.

Nếu câu 3 đúng, tức công tắc 3 điều khiển bóng đèn A hoặc B. Hai câu còn lại sai, đồng nghĩa công tắc 1 nối với A hoặc C, công tắc 2 điều khiển bóng đèn B.

Với dữ kiện này, ta có thể xác định các cặp công tắc - bóng đèn là: 1 - C; 2 - B; 3 - A.