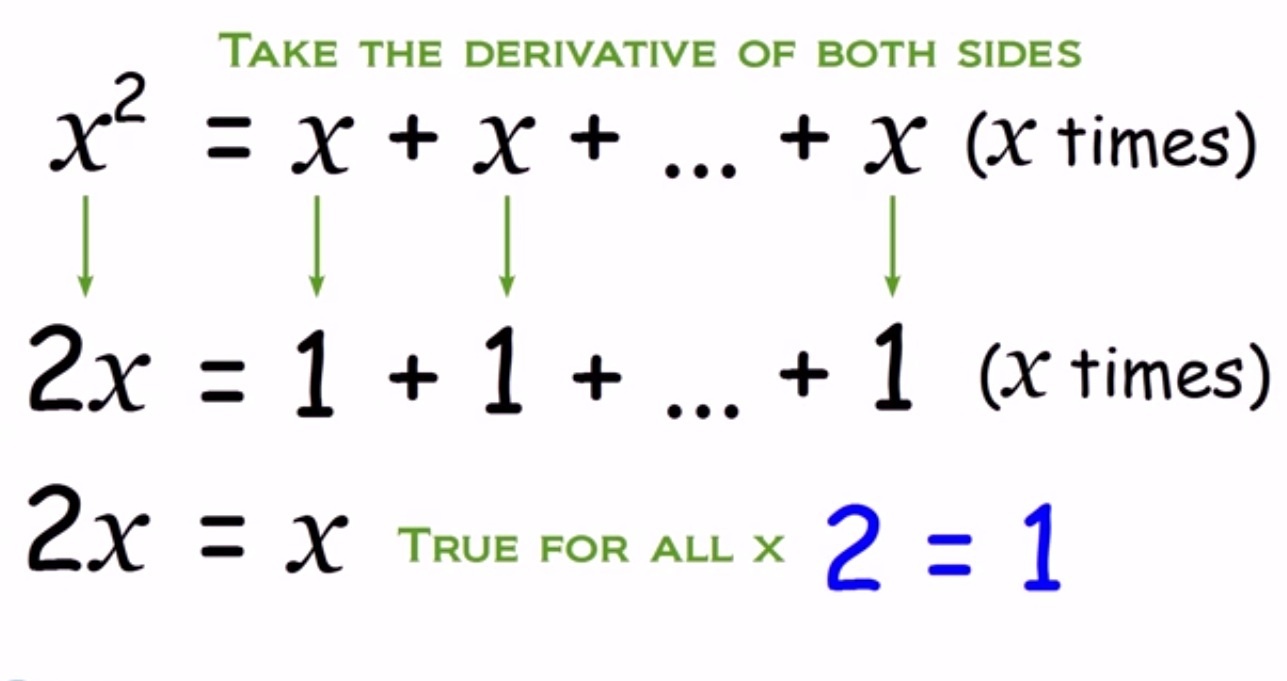Đề bài toán: 1,9999... = 2 đúng hay sai?
Thầy giáo Đỗ Duy Hiếu (Viện Toán học) đưa ra cách giải:
Đặt x = 1,9999..., ta có 10 × x = 19, 9999...
10 × x − x = 19, 9999... − 1, 9999... = 18.
Suy ra: 9 × x = 18. Vậy x = 2, hay 1, 9999... = 2.
Theo thầy giáo Lê Phúc Lữ (luyện thi cho đội tuyển Olympic Toán), cách giải của tác giả Đỗ Duy Hiếu chính xác.
"Trong lập luận có đoạn 10 × x − x = 19, 9999... − 1, 9999... = 18 khiến nhiều người tranh cãi, nhưng theo quan điểm giới hạn thì cách tính đó là hiển nhiên".
Thầy Lữ giải thích, trong sách giáo khoa Toán lớp 7, phần học về Số thập phân vô hạn tuần hoàn đã quy ước 0,1111... (vô hạn chữ số 1) là số thập phân vô hạn được viết là 0,(1) và biểu diễn dưới dạng phân số là 1/9.
Tương tự, số thập phân 1,9999... (vô hạn chữ số 9) sẽ được viết là 1,(9).
Như vậy 1,(9) = 1 + 0,(9) = 1 + 9 × 0,(1) = 1 + 9 × 1/9 = 1 + 1 = 2.
"Nhiều người nghĩ ban đầu số 1,9999... có M chữ số 9, khi 1,9999... × 10 thì còn M-1 chữ số 9. Nhưng ở đây đang xét M là vô hạn nên có trừ đi 1 nó vẫn là vô hạn".
Thầy Lữ cho biết, quy ước 1,9999... (vô hạn số 9) = 2 từ lâu đã được các nhà toán học chấp nhận và được giải thích chi tiết trong bách khoa thư Wikipedia. Tuy nhiên thỉnh thoảng vẫn xuất hiện những ý kiến phản đối quy ước này.
Độc giả có đáp án chính xác
Quan sát các bình luận, thầy Lê Phúc Lữ cho biết, độc giả Trần Việt Anh đã đưa ra cách giải chính xác theo ngôn ngữ giới hạn.
Cách lập luận của Trần Việt Anh:
Trước hết x = 1,9999... là vô hạn số 9. Toán học định nghĩa x chính là giới hạn của dãy số x_n với x_n = 1,99... 9 (có n số 9).
Khi đó x_n = 2 - (0,1)^n. Đặt x = 1,9999... , ta có 10 × x = 19, 9999...
Theo ngôn ngữ giới hạn: 10x = lim (10 x_{n+1}) = lim (20- (0,1)^n)
10x - x = lim (10 x_{n+1} - x_n) = lim [20 - (0,1)^n - 2 + (0,1)^n] = 18. Suy ra: 9 × x = 18. Vậy x = 2, hay 1,9999... = 2.