Mới đây, bài toán trong kỳ thi cuối kỳ của học sinh lớp 3 tại Bảo Lộc (Lâm Đồng) được chia sẻ rộng rãi trong các diễn đàn Toán học.
Đề bài như sau:
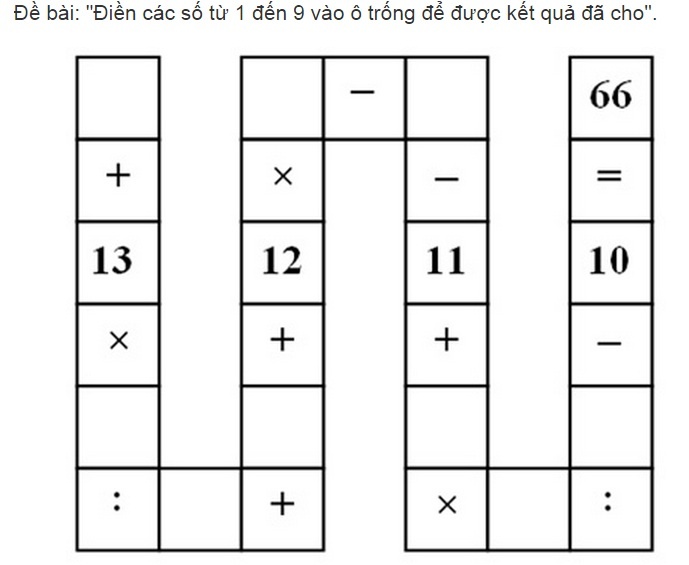 |
Thoạt nhìn bài toán tưởng đơn giản. Tuy nhiên, khi bắt tay vào làm, nhiều thủ khoa, học sinh giỏi Toán, giảng viên đều gặp khó khăn.
Thầy Lại Tiến Minh, giảng viên Đại học Kiến trúc Hà Nội, giáo viên trường THPT Lương Thế Vinh nhận định:
"Đây là bài toán có nhiều nghiệm và yêu cầu của bài toán chỉ cần tìm ra một nghiệm. Tôi đã cho học sinh lớp 10 thực hành bài tập này. Trong gần 60 phút, rất ít học sinh tìm được phương án. Số còn lại “bó tay”.
Cách giải bài toán là theo kiểu mò mẫm, lợi dụng thứ tự ưu tiên giữa các phép toán. Đây là bài toán không hay vì mang tính chất thuộc lòng. Bài toán không có quy luật để giải và không phát huy được năng lực tư duy của học sinh. Đề bài này với học sinh lớp 3 là quá sức".
Đặc biệt, thầy Minh cho rằng, người ra đề đã thực hiện theo cách không giống ai, khi "thực hiện một phép tính ngoài giấy, sau đó xóa đi các số từ 1 - 9, rồi yêu cầu học sinh làm. Và chắc hẳn khi người này đi dạy nếu không có đáp án trước thì khó có thể mò ra kết quả".
Một số nhận xét của các thành viên Gia sư Trực tuyến:
Bùi Văn Cường - sinh viên Đại học Bách khoa Hà Nội – trưởng bộ môn Toán: “Nếu tiến hành đặt ẩn như trên với các ẩn là các số trong khoảng từ 1 đến 9; chúng ta nhận thấy việc giải bài toán này sẽ đưa về một phương trình vô định 9 ẩn. Theo lý thuyết, khi số phương trình ít hơn số ẩn, thường thì sẽ xảy ra trường hợp vô số nghiệm. Trong bài này cũng không ngoại lệ.
Bài toán này không có tính chất toán tiểu học, và lại càng không có tính chất rèn luyện hoặc kích thích tư duy. Có thể việc đặt ra bảng số này là ngẫu hứng với người ra đề, nhưng việc ngẫu hứng này có thể gây hiểu sai lệch vấn đề chương trình giáo dục Toán học lớp 3.
Trần Nguyễn Minh Trân – thủ khoa Đại học Quốc tế (Đại học Quốc gia TP HCM) năm 2014 nhận định: “Chưa rõ đề yêu cầu điền các số tự nhiên từ 1 đến 9 khác nhau hay bất kỳ để thỏa mãn biểu thức. Trường hợp các số khác nhau chắc hẳn sẽ cho ra ít đáp án hơn và đương nhiên sẽ khó hơn rất nhiều. Để tìm ra đáp số cần viết phương trình để tìm ra đáp án. Tuy nhiên kỹ năng này học sinh lớp 3 không có được”.
Trần Trí Kiên - sinh viên Đại học Ngoại thương, từng đạt giải nhì quốc gia môn Toán cho biết, bài toán tưởng chừng đơn giản nhưng không phải.
“Về mặt nguyên tắc, bài toán chỉ có các phép tính +, -, ×,÷ và các con số trong giới hạn 100, hoàn toàn phù hợp học sinh lớp 3. Tuy nhiên, khi bắt tay vào bài toán này, người giải lại gặp phải hết khó khăn này đến khó khăn khác.
Nếu đặt các ô trống trong phép tính thành các ẩn a,b,c,…,h,i, thì bài toán trở thành một phương trình có tới 8 ẩn (theo câu chữ trong đề bài có thể ngầm hiểu là đôi một khác nhau). Việc đầu tiên mà ta nghĩ đến là thay "đại" một vài bộ số.
Tuy nhiên ta sẽ nhanh chóng nhận ra rằng, việc thay như vậy chẳng khác nào mò kim đáy bể. Những người có chút hiểu biết về số học sẽ bắt tay vào sử dụng phép chia hết, tính chẵn lẻ, phép đồng dư để thu hẹp các trường hợp, nhưng cũng không đem lại kết quả đáng kể.
Khi mọi việc trở nên khó khăn, nhiều người sẽ nghĩ rằng, "phải chăng đề bài có vấn đề", và họ lại sử dụng các kiến thức số học trên, thậm chí cả một số kiến thức cao hơn như hệ thặng dư trung hoa… để tìm cách chứng minh đề bài sai. Tuy nhiên, mọi nỗ lực "chứng minh đề bài sai" này cũng đều không đi đến kết quả.
Phương pháp duy nhất tìm ra đáp án là thử nhiều hơn nữa các bộ số (sau khi đã thu hẹp các trường hợp) với hy vọng sẽ tìm ra đáp án.