Bí quyết giải các bài toán liên quan thiết diện

Ảnh: Giáo dục Thời đại.

Giúp học sinh vượt qua dạng bài tập này, giáo viên Nguyễn Ngọc Minh (trường THPT Nguyễn Siêu, Hưng Yên) đưa các kiến thức cơ bản; phân tích các phương pháp dựng thiết diện (trường hợp tổng quát, có quan hệ song song, quan hệ vuông góc); đồng thời, đi vào hai bài toán cụ thể liên quan thiết diện.

Những kiến thức cần nhớ

Với các bài toán liên quan thiết diện, học sinh cần nắm vững kiến thức cơ bản như sau:

Khái niệm thiết diện (mặt cắt): Cho hình T và mặt phẳng (P), phần mặt phẳng của (P) nằm trong T được giới hạn bởi các giao tuyến sinh ra do (P) cắt một số mặt của T được gọi là thiết diện (mặt cắt).

Hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng nếu có cũng song song với hai đường thẳng ấy hoặc trùng một trong hai đường thẳng đó.

Hai mặt phẳng phân biệt cùng song song một đường thẳng thì giao tuyến của chúng nếu có cũng song song với đường thẳng đó.

Các cách xác định mặt phẳng: Biết ba điểm không thẳng hàng; hai đường thẳng cắt nhau; một điểm nằm ngoài một đường thẳng; hai đường thẳng song song.

Lưu ý một số nội dung sau: Giả thiết mặt phẳng cắt là (P), hình đa diện là T. Dựng thiết diện là bài toán dựng hình nhưng chỉ cần nêu phần dựng và phần biện luận nếu có.

Đỉnh của thiết diện là giao của mặt phẳng (P) và các cạnh của hình T nên việc dựng thiết diện thực chất là tìm giao điểm của (P) và các cạnh của T.

Mặt phẳng (P) có thể không cắt hết các mặt của T. Các phương pháp dựng thiết diện được đưa ra tùy thuộc dạng giả thiết của đầu bài.

Các bài toán liên quan thiết diện thường là: Tính diện tích thiết diện; tìm vị trí mặt phẳng (P) để thiết diện có diện tích lớn nhất, nhỏ nhất; thiết diện chia khối đa diện thành 2 phần có tỉ số cho trước.(hoặc tìm tỉ số giữa 2 phần).

Một số phương pháp dựng thiết diện

Mặt phẳng (P) cho dạng tường minh: Ba điểm không thẳng hàng, hai đường thẳng cắt nhau hoặc một điểm nằm ngoài một đường thẳng...:

Phương pháp giải như sau: Trước tiên, tìm cách xác định giao tuyến của (P) với một mặt của T (thường được gọi là giao tuyến gốc).

Trên mặt phẳng này của T, tìm thêm giao điểm của giao tuyến gốc và các cạnh của T nhằm tạo ra thêm một số điểm chung. Lặp lại quá trình này với các mặt khác của T cho tới khi tìm được thiết diện.

Mặt phẳng (P) đi qua d và song song với đường thẳng d, chéo nhau với đường thẳng l:

Phương pháp giải như sau: Trên (P) mới có đường thẳng d, để (P) xác định, dựng đường thẳng d’ cắt d và d’ // l.

Cách dựng: Chọn một mặt phẳng (Q) chứa d sao cho giao điểm A của d và (Q) dựng được ngay. Trong mặt phẳng (Q) ta dựng d’ qua A và d’ // d khi đó (P) xác định bởi hai đường thẳng cắt nhau d và d’.

Mặt phẳng (P) đi qua một điểm M song song với hai đường thẳng chéo nhau d và l:

Phương pháp giải: Xét 2 mặt phẳng (M, d) và (M, l) mỗi mặt phẳng này chứa một đường thẳng qua M song song với d và l. Mặt phẳng (P) là mặt phẳng chứa hai đường thẳng vừa dựng.

Mặt phẳng (P) qua điểm M và song song với mặt phẳng (Q):

Phương pháp giải: Dựa vào tính chất “Nếu một mặt phẳng cắt một trong hai mặt phẳng song song thì phải cắt mặt phẳng còn lại và giao tuyến của chúng song song”.

Tìm thêm giao điểm của a’ với các cạnh của đa giác trong (R). Tiếp tục quá trình với các giao điểm mới cho tới khi dựng được thiết diện.

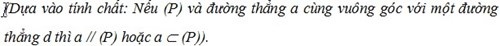Mặt phẳng (P) đi qua một điểm M và vuông góc với một đường thẳng d:

Phương pháp giải: Tìm hai đường thẳng a và a’ cùng vuông góc với d khi đó (P) là mặt phẳng qua M song song với a và a’. 

Mặt phẳng (P) đi qua một đường thẳng d và vuông góc với một đường thẳng l:

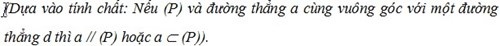Phương pháp giải: Dựng mặt phẳng phụ (Q) chứa l và vuông góc với d tại một điểm M.

Trong (Q) dựng qua M đường thẳng vuông góc với l tại H khi đó mặt phẳng (P) là mặt phẳng (H, d).

Mặt phẳng (P) đi qua đường thẳng d và vuông góc với mặt phẳng (Q) đã cho (d xiên góc với (Q)):

Các bài toán liên quan đến thiết diện

Tính diện tích thiết diện, xác định vị trí mặt phẳng cắt để thiết diện có diện tích lớn nhất, nhỏ nhất:

Với bài toán này, cần lưu ý: Thiết diện là đa giác nằm trong mặt phẳng cắt nên tính diện tích thiết diện là tính diện tích đa giác trong mặt phẳng. Vì vậy, có thể áp dụng tất cả các phương pháp đã biết về tính diện tích đa giác trong mặt phẳng để tính:

Tính tỉ số thể tích 2 phần khối đa diện bị chia bởi thiết diện hoặc tính thể tích một trong 2 khối đa diện được tạo ra bởi thiết diện:

Một mặt phẳng chia khối chóp T ra làm hai phần là T₁, T₂. Khi đó ta cần xác định tỉ số thể tích của hai phần thì phải làm thế nào?

Thể tích là vấn đề của chương trình lớp 12 nên phần này tác giả sẽ giới thiệu một số bài tập, để đi sâu vào vấn đề này tác giả sẽ viết trong một đề tài khác.

Một số lưu ý về kiến thức liên quan: