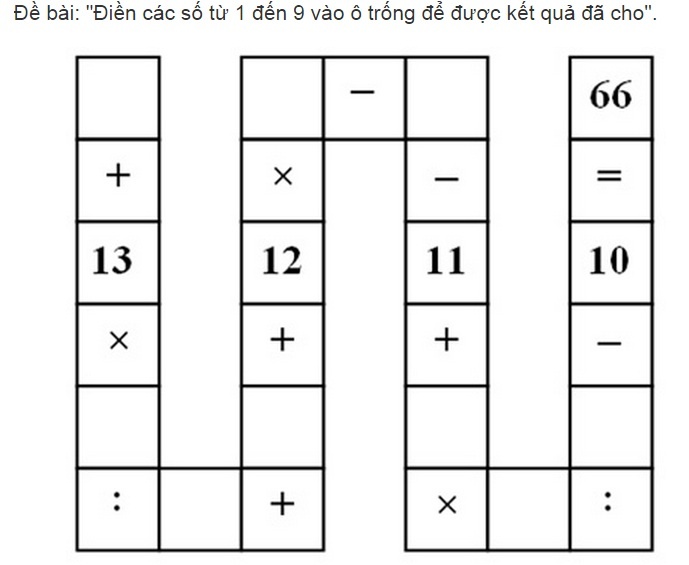
Mới đây, bài toán trong kỳ thi cuối kỳ của học sinh lớp 3 tại Bảo Lộc (Lâm Đồng) được chia sẻ rộng rãi trong các diễn đàn Toán học.
Đề bài như sau:
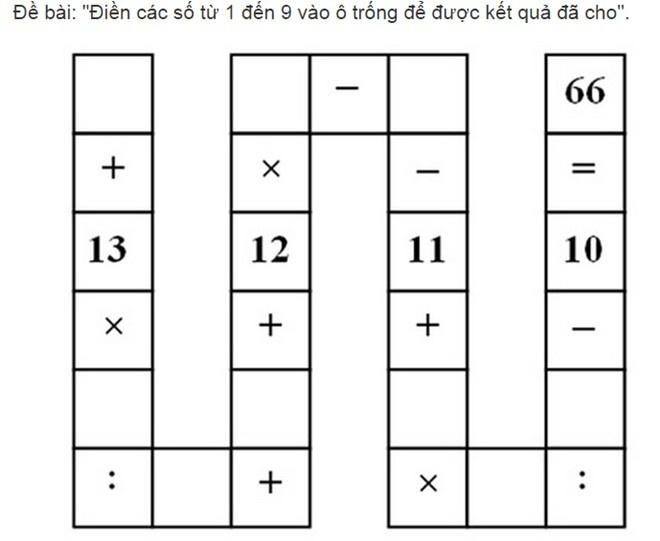 |
Thoạt nhìn bài toán tưởng đơn giản. Tuy nhiên, khi bắt tay làm, nhiều thủ khoa, học sinh giỏi Toán, giảng viên đều gặp khó khăn.
Thầy Lại Tiến Minh, giảng viên Đại học Kiến trúc Hà Nội, giáo viên trường THPT Lương Thế Vinh nhận định: "Đây là bài toán có nhiều nghiệm và yêu cầu của bài toán chỉ cần tìm ra một nghiệm. Cách giải bài toán là theo kiểu mò mẫm, lợi dụng thứ tự ưu tiên giữa các phép toán".
Thầy Minh cho rằng, bài toán chỉ mang tính chất thuộc lòng, không phát huy được năng lực tư duy của học sinh.
"Người ra đề đã thực hiện theo cách không giống ai, khi "thực hiện một phép tính ngoài giấy, sau đó xóa đi các số từ 1 - 9, rồi yêu cầu học sinh làm. Và chắc hẳn khi người này đi dạy nếu không có đáp án trước thì khó có thể mò ra kết quả" - thầy Minh nhận xét.
Gợi ý một số cách giải bài toán như sau:
Bùi Văn Cường - sinh viên Đại học Bách khoa Hà Nội - trưởng bộ môn Toán, Gia sư Trực tuyến đã viết chương trình trên máy tính giải bài toán trong 5 phút, chạy trong nửa giây. Cường cho biết, để thực hiện chương trình này cần trình độ sinh viên đại học, hoặc học sinh tự học ngôn ngữ lập trình trong 3 tháng.
"Đặt thứ tự các số cần tìm như sau:
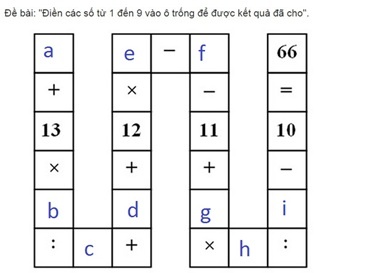 |
Nếu tiến hành đặt ẩn như trên với ẩn là các số trong khoảng từ 1 đến 9; ta nhận thấy, việc giải bài toán trên sẽ đưa về một phương trình vô định 9 ẩn.
Theo lý thuyết, khi số phương trình ít hơn số ẩn, thường sẽ xảy ra trường hợp vô số nghiệm. Trong bài này cũng không ngoại lệ. Bài toán có vô số đáp số cho dù các ẩn số chỉ được gói gọn trong điều kiện là các chữ số.
Thực vậy, nếu viết ra dưới dạng phương trình, ta sẽ thu được:
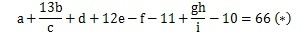 |
Dưới quan điểm hoán vị, ta thấy 2 ẩn g và h có vai trò tương đương nhau trong phương trình (*) trên, do đó, ít nhất bài toán nếu có nghiệm, sẽ có ít nhất hai nghiệm. (1)
Với một phương trình vô định có nhiều ẩn, việc giải nó không bao giờ dễ dàng, vì không có đủ các điều kiện ràng buộc giữa các ẩn. (2).
Vì vậy, chúng ta phải dùng đến công cụ giải là máy tính (computer, không phải calculator). Nên chúng ta có thể viết một chương trình chuyên biệt để giải bài toán này với 9 ẩn như đã trình bày. Ở đây, chúng tôi sử dụng ngôn ngữ lập trình C++, viết chương trình bằng DEV – C++ để giải bài toán trên.
Mã nguồn sơ bộ:
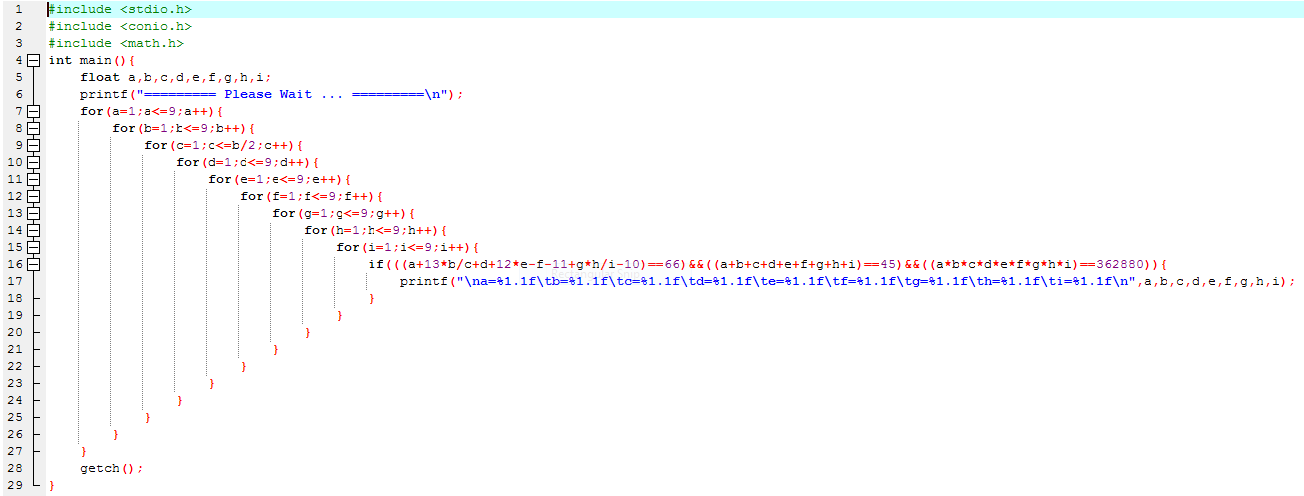 |
Nói một chút về chuyên môn, chương trình trên sử dụng 9 vòng lặp for để quét tất cả các trường hợp có thể và in ra màn hình tất cả bộ giá trị thỏa mãn đề bài. Do đó, nếu coi các phép toán so sánh và số học là những phép toán cơ bản, thì thời gian chạy của chương trình trên ước tính là O(n^9 ) (với n là phạm vi của ẩn số từ 0 đến n).
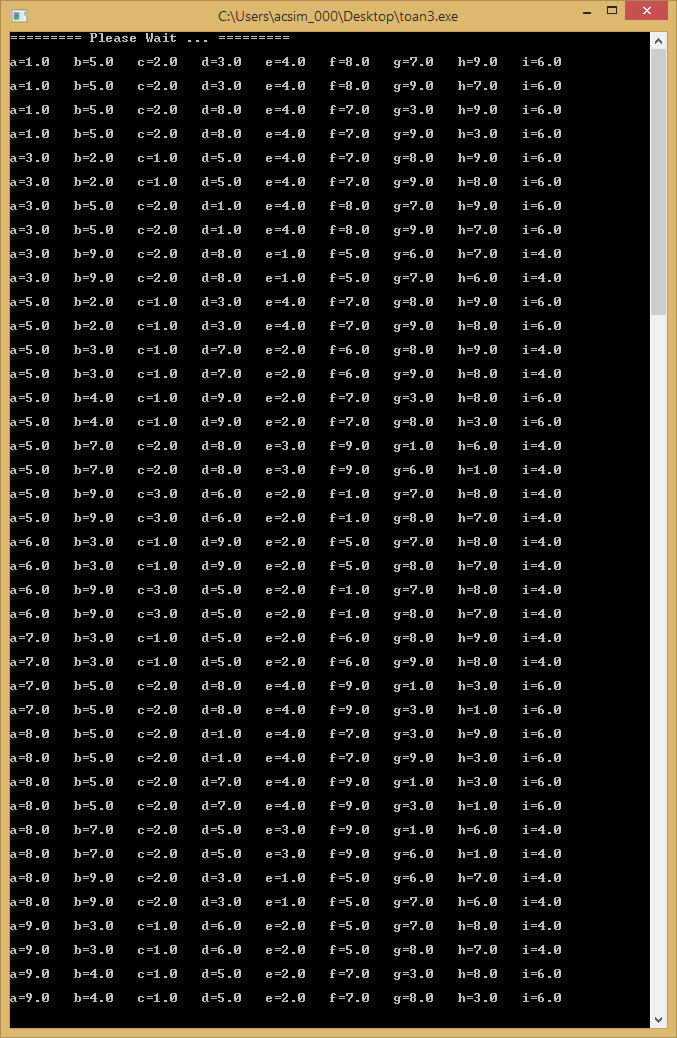
Kết quả thực hiện chương trình cho ra vô số bộ giá trị thỏa mãn bài toán. Đây là phần kết quả thực hiện trên máy tính với bộ VXL Intel Core i7 – 4510U. Cũng may là trong bài này n = 9. (3)
Từ các kết quả (1), (2) và (3), có thể thấy, bài toán này không phù hợp học sinh lớp 3. Ngay cả với người bình thường, việc liệt kê tất cả các bộ giá trị đóng vai trò lời giải cho bài toán trên là điều gần như không thể.
Có 9 ẩn, do đó có 9!=362880 cách thử chọn số, trong khi số kết quả thỏa mãn lại chỉ chưa đến 50; nên có thể nói việc thử lần lượt trường hợp cũng đã là việc làm mò kim đáy bể.
Vì vậy, bài toán này không có tính chất toán tiểu học và lại càng không có tính chất rèn luyện hoặc kích thích tư duy. Có thể việc đặt ra bảng số này là ngẫu hứng với người ra đề, nhưng việc ngẫu hứng này có thể gây hiểu sai lệch vấn đề chương trình giáo dục Toán học lớp 3.
 |
Trần Nguyễn Minh Trân – thủ khoa Đại học Quốc tế (Đại học Quốc gia TP HCM) năm 2014:
"Chưa rõ đề yêu cầu điền các số tự nhiên từ 1 đến 9 khác nhau hay bất kỳ để thỏa mãn biểu thức. Trường hợp các số khác nhau chắc hẳn sẽ cho ra ít đáp án hơn và đương nhiên sẽ khó hơn rất nhiều. Trường hợp này có thể viết chương trình chạy sẽ tìm được các đáp án.
 |
Còn nếu các số bất kỳ thì dễ hơn, và chắc chắn sẽ có rất rất nhiều đáp án. Để đáp ứng đề bài, chúng ta chỉ cần thử các giá trị, để đơn giản hóa, ta có thể viết lại như sau:
Gọi các số cần tìm là a1, a2,…, a9
Ta có a1 + (13 x a2 : a3) + a4 + (12 x a5) – a6 - 11 + (a7 x a8 : a9) – 10 = 66
Cho a1 = a2 = a3 = a4 = a6 = a7 = a8 = a9 = 1, ta được 12 x a5 = 72 suy ra a5 = 6".