Người đầu tiên đoạt HCB Toán quốc tế giải bài lớp 3

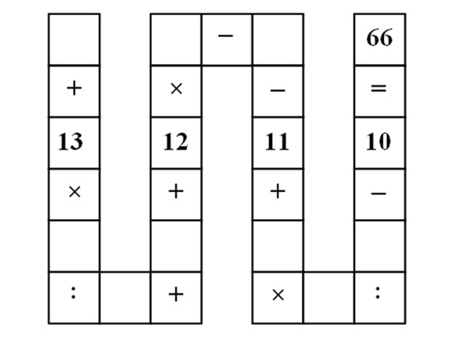
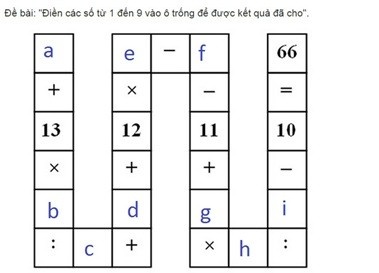
Đặt thứ tự các số cần tìm như sau:

- Bằng lập trình, với giả định là các số trong ô có thể bằng nhau và các phép chia trong các ô đều nguyên, bài toán có tất cả 351.020 lời giải. Chẳng hạn một lời giải là:

1 + 13 x 1 : 1 + 2 + 12 x 6 - 2 - 11 + 1 x 2 : 2 - 10 = 66.

- Bằng kiến thức học sinh cấp 3, đặt giá trị các ô chưa biết lần lượt là a, b, d, e, f, g, h và i, ta có thu được một biểu thức như sau:

a + 13 x b : c + d +12 x e - f -11 + g x h : i -10 = 66.

Sau đó rút gọn được biểu thức sau:

a + 13 x b : c +d +12 x e - f + g x h : i =87.

Đặt x = b : c (chắc chắn phải nguyên, do 13 là số nguyên tố), y = e, z = a + d - f + g x h : i, tôi có phương trình nghiệm nguyên sau:

13x + 12 y + z = 87.

Phương trình loại này có công thức để tìm ra nghiệm, nhưng nếu không sử dụng kiến thức cao cấp, tôi thấy không đơn giản lắm. Ta có thể đi tiếp bằng cách thử với x = 1, và thu được 12y + z = 74. Có thể đem chia 74 cho 12 được thương là 6, dư 2, và như vậy chỉ còn cần chọn các giá trị sao cho có

b:c = x = 1.

e = y = 6.

a + d - f + g x h : i = 2.

Với điều kiện là các chữ cái chỉ tương ứng với các số từ 1 đến 9.

Đến đây, bài toán không còn khó với một học sinh cấp 3 nữa, nhưng tôi cho rằng vẫn còn khó với một học sinh lớp 3. Tất cả những bước thử nghiệm trên đòi hỏi học sinh phải có một tư duy toán học thật sự.

Khi theo dõi quá trình giải này, các bạn thấy bài toán không đơn giản, ngay cả khi ta sử dụng các công cụ của học sinh cấp 3.

- Tuy nhiên, có thể nói bài toán này kiểm tra năng khiếu của học sinh. Học sinh có thể giải bằng cách mò mẫm, điền thử số vào các ô và điều chỉnh sao cho cuối cùng có lời giải. Trong trường hợp đó, bài toán này vẫn khó vì số lượng các ô cần điền khá nhiều, thử không dễ dàng. Vì thế, không thể đưa ra trong cuốn sách giáo khoa hoặc trong một bài kiểm tra thông thường.

- Còn một vấn đề nữa về cách hiểu bài toán. Tôi thấy đầu bài nói ngắn gọn quá, khiến người đọc không thật rõ ý định. Trên mạng, nhiều bạn đọc cho rằng, có thể đầu bài đòi hỏi là mỗi số từ 1 đến 9 được sử dụng đúng 1 lần, vì có đúng 9 ô trống. Nếu hiểu như vậy, thì bài toán sẽ còn khó hơn. Bằng lập trình, ta thấy có đúng 20 lời giải khác nhau:

Lời giải 1 là: 3+13*2/1+5+12*4-7-11+8*9/6-10=66.

Lời giải 2 là: 3+13*2/1+5+12*4-7-11+9*8/6-10=66.

Lời giải 3 là: 5+13*2/1+3+12*4-7-11+8*9/6-10=66.

Lời giải 4 là: 5+13*2/1+3+12*4-7-11+9*8/6-10=66.

Lời giải 5 là: 5+13*3/1+7+12*2-6-11+8*9/4-10=66.

Lời giải 6 là: 5+13*3/1+7+12*2-6-11+9*8/4-10=66.

Lời giải 7 là: 5+13*4/1+9+12*2-7-11+3*8/6-10=66.

Lời giải 8 là: 5+13*4/1+9+12*2-7-11+8*3/6-10=66.

Lời giải 9 là: 5+13*9/3+6+12*2-1-11+7*8/4-10=66.

Lời giải 10 là: 5+13*9/3+6+12*2-1-11+8*7/4-10=66.

Lời giải 11 là: 6+13*3/1+9+12*2-5-11+7*8/4-10=66.

Lời giải 12 là: 6+13*3/1+9+12*2-5-11+8*7/4-10=66.

Lời giải 13 là: 6+13*9/3+5+12*2-1-11+7*8/4-10=66.

Lời giải 14 là: 6+13*9/3+5+12*2-1-11+8*7/4-10=66.

Lời giải 15 là: 7+13*3/1+5+12*2-6-11+8*9/4-10=66.

Lời giải 16 là: 7+13*3/1+5+12*2-6-11+9*8/4-10=66.

Lời giải 17 là: 9+13*3/1+6+12*2-5-11+7*8/4-10=66.

Lời giải 18 là: 9+13*3/1+6+12*2-5-11+8*7/4-10=66.

Lời giải 19 là: 9+13*4/1+5+12*2-7-11+3*8/6-10=66.

Lời giải 20 là: 9+13*4/1+5+12*2-7-11+8*3/6-10=66.

Lại có ý kiến khác nữa: Các ô được xếp thành dãy khó quan sát như vậy thì phải chăng họ muốn thực hiện các phép toán theo thứ tự của các ô (như kiểu bấm máy tính cầm tay). Chẳng hạn một lời giải theo cách hiểu đó là (((9+13) x 3 : 1 + 9 + 12) x  1 -1 -11 +1) x 1:1 -10=66.

Tôi nghĩ, đề bài toán cần phải diễn đạt thật rõ ràng để tránh cho học sinh không thể hiểu nhầm. Trong bài toán trên, người ra đề nên viết thêm cho rõ nghĩa. Chẳng hạn, nếu các số trong các ô có thể bằng nhau, thì cũng nên nói điều đó trong đề bài.

Ở đây, tôi có nghi ngờ là đề bài toán gốc (bài toán này có thể lấy từ nguồn nào đó) có điều kiện các số trong các ô khác nhau là khác nhau (vì khi đó bài toán mới thật sự hấp dẫn về mặt toán học).